Bayes'sche Optimierung (German)

Alexander Schoch,•programmingpythongermanmachine learningalgorithm
Back
gaussian regression banner art

Bayes’sche Optimierung ist eine Methode, das Maximum einer Zielfunktion zu finden, die unbekannt und teuer zum Evaluieren ist.

Beispiel: Wir möchten eine chemische Reaktion optimieren, die einen Stoff C herstellt. Um das Produkt zu maximieren, müssen wir die Temperatur finden, bei welcher die Reaktion am meisten C produziert (also sie die grösste Ausbeute hat). Entsprechend gibt es eine Funktion Y(T)Y(T), welche Ausbeute und Temperatur korreliert, aber wir kennen diese Funktion nicht. Es wäre zwar möglich, ganz viele Reaktionen an verschiedenen Temperaturen zu messen, aber das würde ewig dauern, da eine Reaktion (= Sample) beispielsweise zwei Tage dauern könnte.

Das Ziel der Bayes’schen Optimierung ist es, das Maximum einer Funktion (hier: die Temperatur mit maximaler Ausbeute) zu finden und dabei so wenig Datenpunkte wie möglich zu messen. Spezifischer berechnet BO das wahrscheinlichste Maximum mit einer bestimmten Anzahl an Evaluierungen.

Wie funktioniert BO?

BO führt der Reihe nach die folgenden Schritte aus:

Anfangsdaten

Bevor wir mit BO starten, evaluieren wir die Funktion NN mal, wobei NN eine positive Ganzzahl ist. Zu Beginn wissen wir noch nicht, wo das Optimum sein könnte und wie die Funktion aussehen könnte. Entsprechend macht es Sinn, mal mit ein paar Anfangsdaten zu starten.

Zielfunktion mit drei schon gemessenen Datenpunkten.

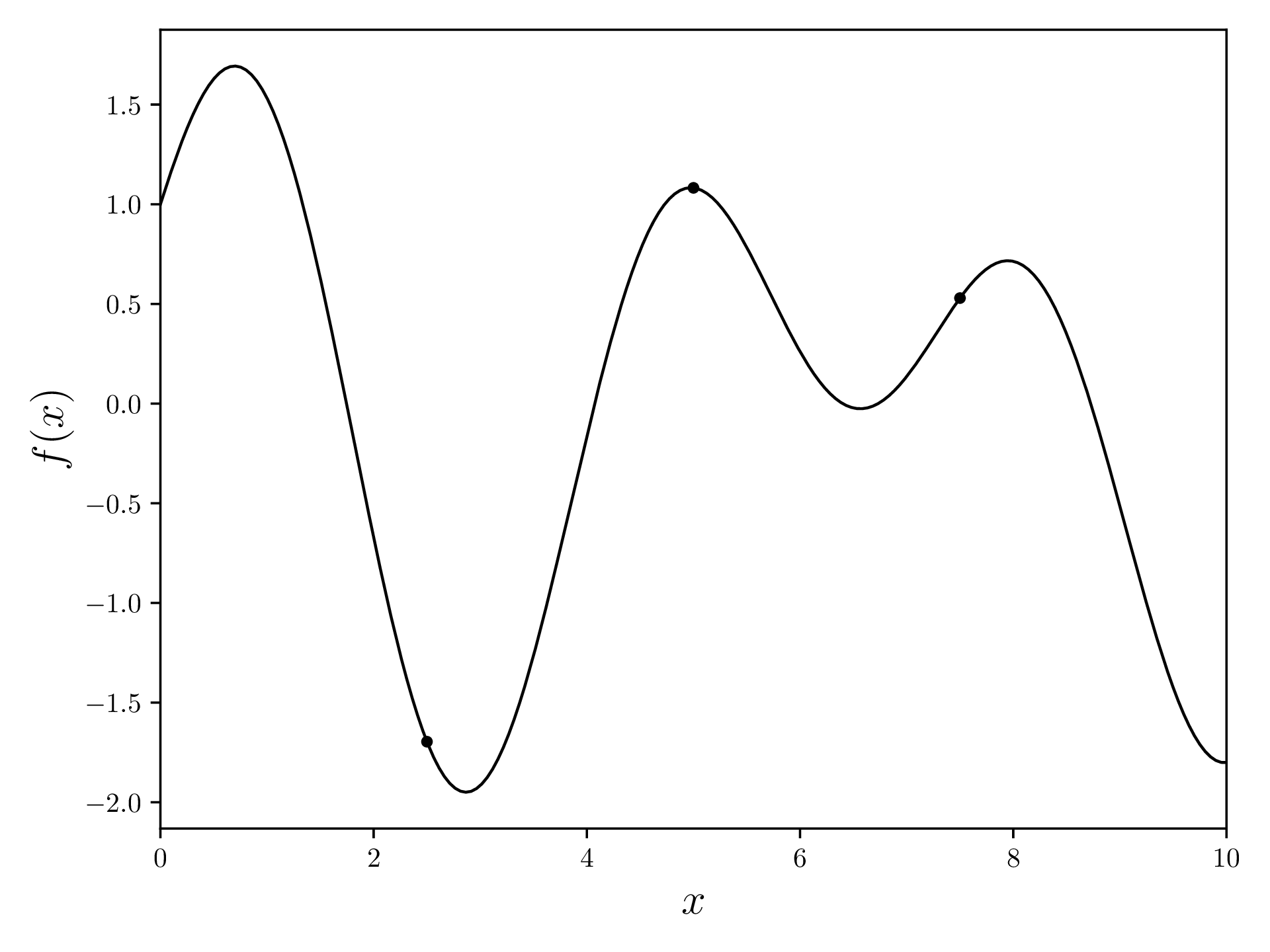
Hauptloop

Nun wiederholen wir die folgenden Schritte, bis entweder

Surrogatmodell

Nun ziehen wir ein Surrogatmodell durch die Punkte, die schon gemessen wurden. Dieses Modell versucht abzuschätzen, was die Zielfunktion sein könnte und weist jedem Punkt einen Mittelwert und eine Standardabweichung zu. Das Surrogatmodell ist nah bei Datenpunkten sehr präzise (tiefe Standardabweichung). Das macht intuitiv Sinn: Punkte, die wir schon kennen, sind “fixiert” und entsprechend ist in deren Nähe nicht viel Spielraum.

Es gibt viele Methoden für diese Aufgabe, aber die meisten BO-Implementierungen benutzen einen Gauss-Prozess, auch “Kriging” genannt.

Surrogatmodell mit Mittelwert und Standardabweichung für drei Datenpunkte.

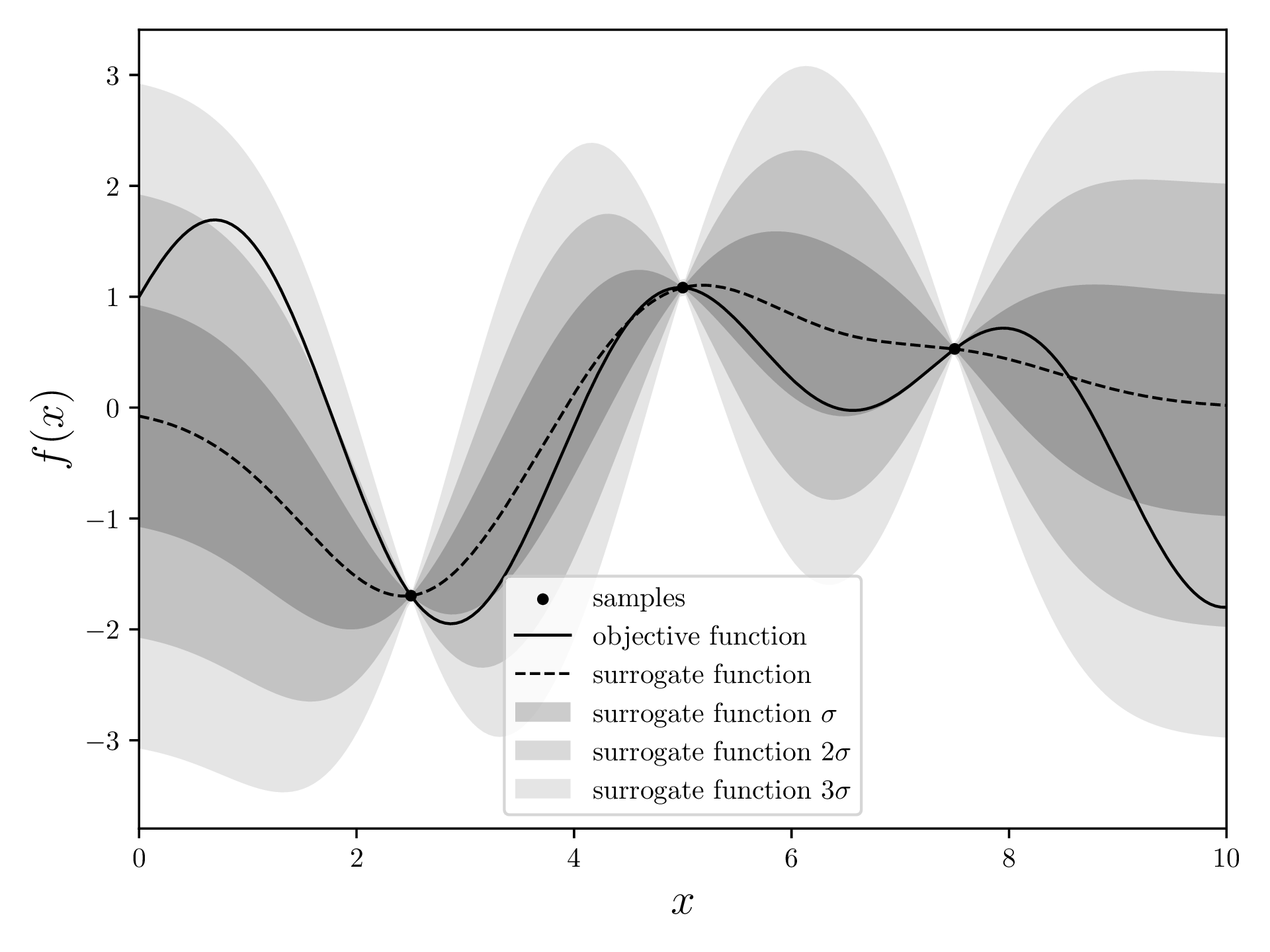
Akquisitionsfunktion

Als nächstes versuchen wir, herauszufinden, wo ein nächster Datenpunkt am meisten Sinn machen könnte. Es gibt verschiedene Akquisitionsfunktionen (AF), die wir benutzen können. Eine der Häufigsten ist aber “Erwartete Verbesserung” (EI, von “Expected Improvement”). Diese AF berechnet für jedes xx den Erwartungswert der Verbesserungsfunktion von f(x)f(x).

Die EI vom Beispiel oben sieht so aus:

Erwartete Verbesserung des Surrogatmodells oben

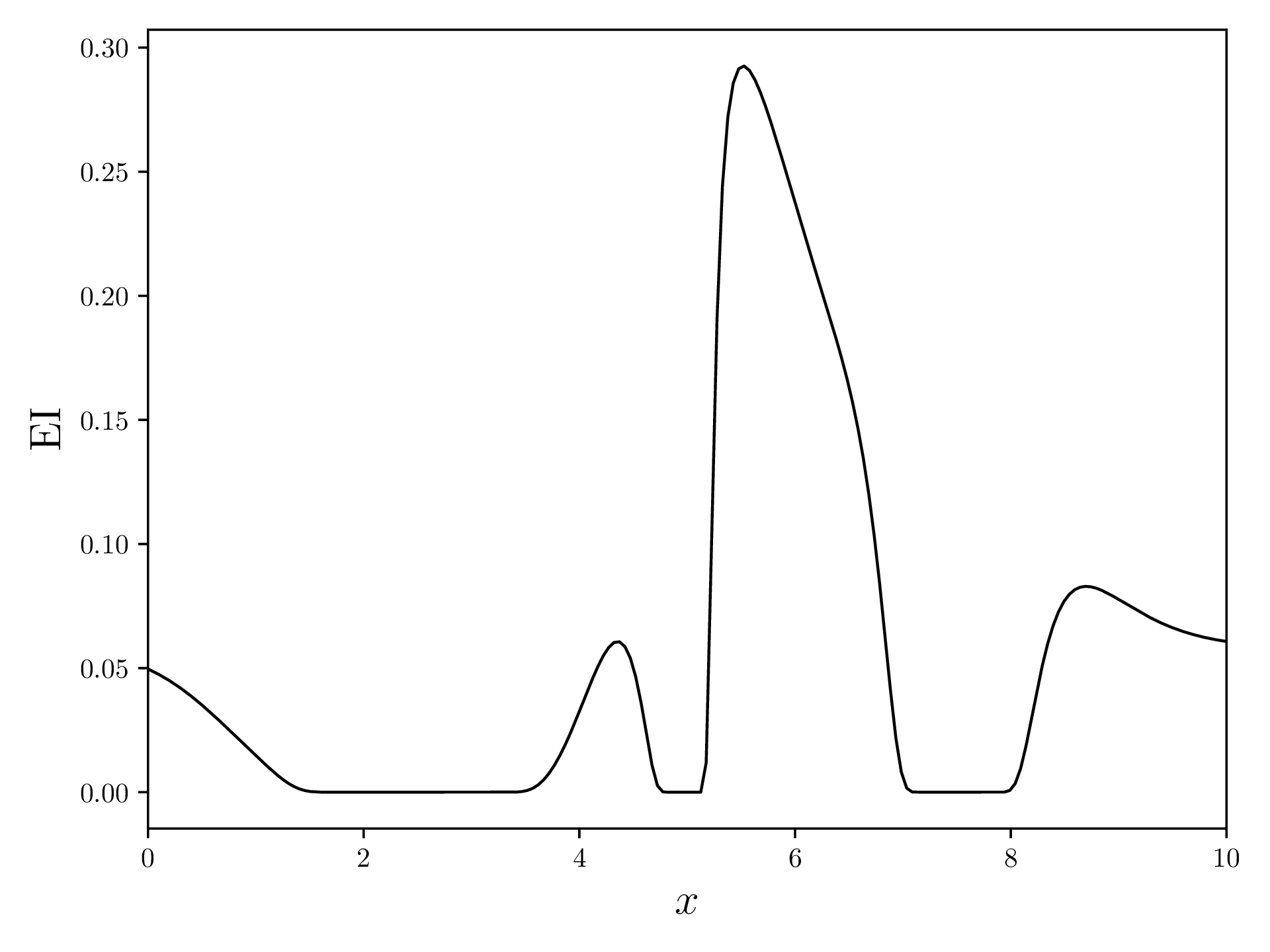
Messung eines neuen Datenpunktes

Die Akquisitionsfunktion sagt uns nun, wo der beste Punkt für eine nächste Messung liegt. Dafür nehmen wir das Maximum der AF und benutzen dessen xx-Wert, um die Zielfunktion erneut zu evaluieren.

Resultat

Nachdem der Hauptloop fertig ist, berechnen wir das Surrogatmodell noch einmal und geben das Maximum dieses Modells zurück. Dies ist das (wahrscheinlichste) Maximum der Zielfunktion. In diesem Fall ist das Maximum bei x∗=0.704x^* = 0.704 mit einem Maximum von f(x∗)=1.693f(x^*) = 1.693.

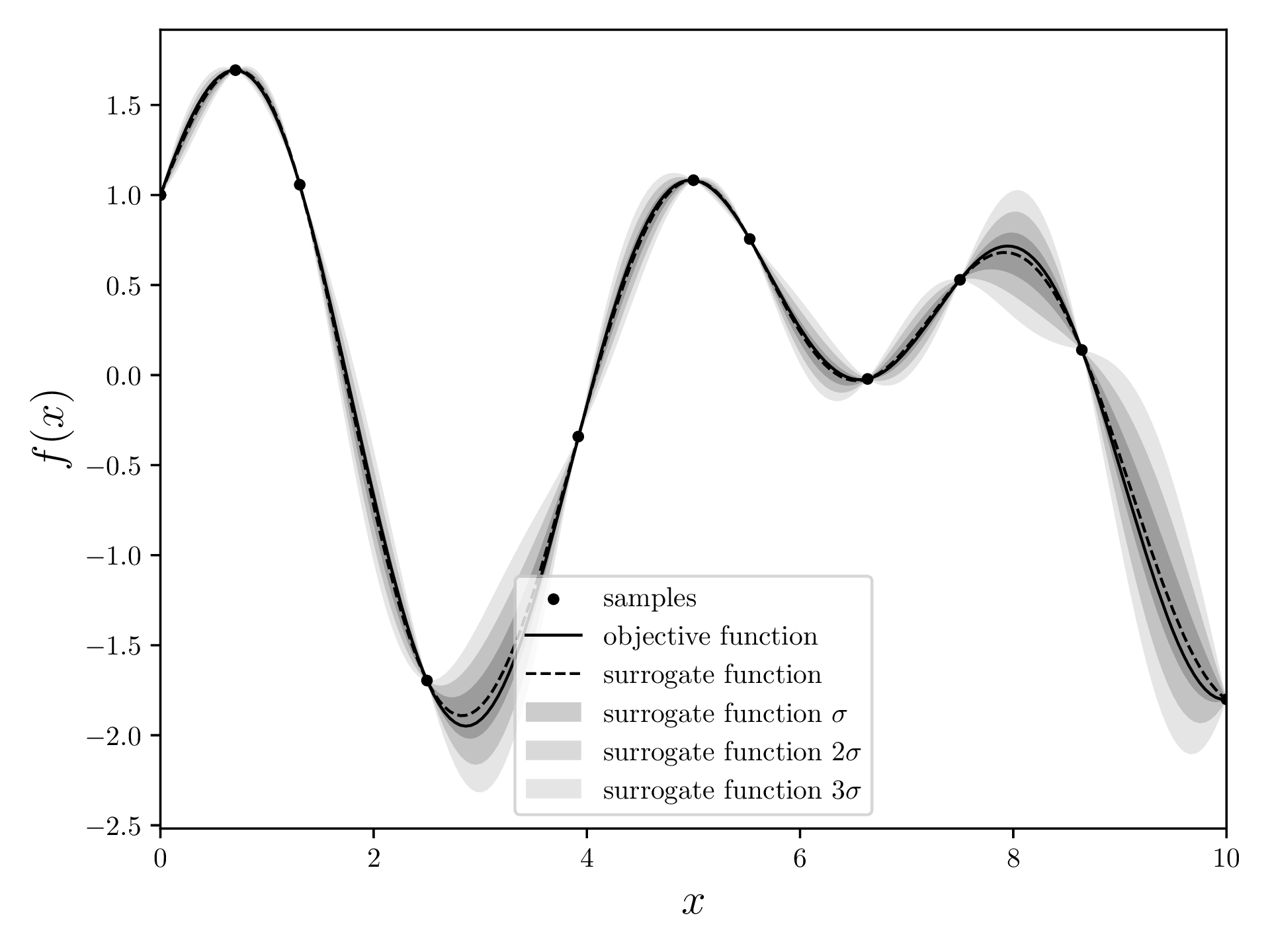
Surrogatmodell nach 10 Iterationen

Implementierung

Erstelle zunächst ein neues Python-venv, aktiviere dieses und installiere alle nötigen Bibliotheken.

python -m venv venv
source venv/bin/activate # OS-abhängig
 
pip install numpy scipy matplotlib

Erstelle nun ein neues Python-File und importiere alle nötigen Bibliotheken.

import os
import numpy as np
import matplotlib.pyplot as plt
 
from functools import reduce
from scipy.stats import norm

Als nächstes definieren wir einige Konstanten für später. DOMAIN ist das Ausmass der xx-Achse, INITIAL_SAMPLES definiert, wie viele Punkte wir zu Beginn evaluieren möchten, BUDGET ist die Anzahl Iterationen und machine_epsilon wird später relevant.

DOMAIN=[0,10]
INITIAL_SAMPLES=3
BUDGET=10
 
machine_epsilon = np.finfo(np.float32).eps

Zielfunktion

So, definieren wir eine Zielfunktion, welche unser BO optimieren soll. In diesem Beispiel benutze ich

f(x)=sin⁡1.7x+cos⁡x,f(x) = \sin 1.7x + \cos x,

weil diese ein klares Maximum hat und einigermassen interessant ausschaut.

objective_function = lambda x: np.sin(1.7 * x) + np.cos(x)

Nun evaluieren wir diese Funktion drei Mal an äquidistanten Positionen.

samples = np.array([[x, objective_function(x)] for x in np.linspace(*DOMAIN, INITIAL_SAMPLES+2)[1:-1]])
[[ 2.5        -1.69613297]
 [ 5.          1.0821493 ]
 [ 7.5         0.52923445]]

Plotte nun die Zielfunktion mit den Datenkpunkten. Weil samples ein Array von [x, y] ist, transponieren (.T) wir und nehmen die Spalten fürs Plotting.

fig, ax = plt.subplots(figsize=(12.8, 4.8))
 
xvalues = np.linspace(*DOMAIN, 200)
yvalues = objective_function(xvalues)
 
ax.plot(xvalues, yvalues, linewidth=1, color='black')
ax.scatter(*samples.T, s=10, c='black')
ax.set_xlabel(r'$x$', fontsize=16)
ax.set_ylabel(r'$f(x)$', fontsize=16)
ax.set_xlim(*DOMAIN)
 
plt.tight_layout()
os.makedirs('output', exist_ok=True)
plt.savefig(os.path.join('output', 'objective_function.pdf'))
plt.close('all')
Zielfunktion mit drei Datenkpunkten

Surrogatmodell (Gauss-Prozess)

Kovarianz

Für den Gauss-Prozess brauchen wir zunächst eine Kovarianzfunktion. Diese Funktion berechnet aus zwei Punkten x1x_1 und x2x_2 einen Wert, welcher beschreibt, wie gut diese Werte korrellieren. Für diese Demonstration verwenden wir den Filter quadratische Exponentialfunktion, welcher eine hohe Korrelation für örtlich nache Punkte zurückgibt.

Die quadratische Exponentialfunktion ist definiert als (Quelle )

K(x1,x2)=exp⁡−12∣x1−x2∣2K(x_1, x_2) = \exp -\frac{1}{2}|x_1 - x_2|^2

und sieht so aus:

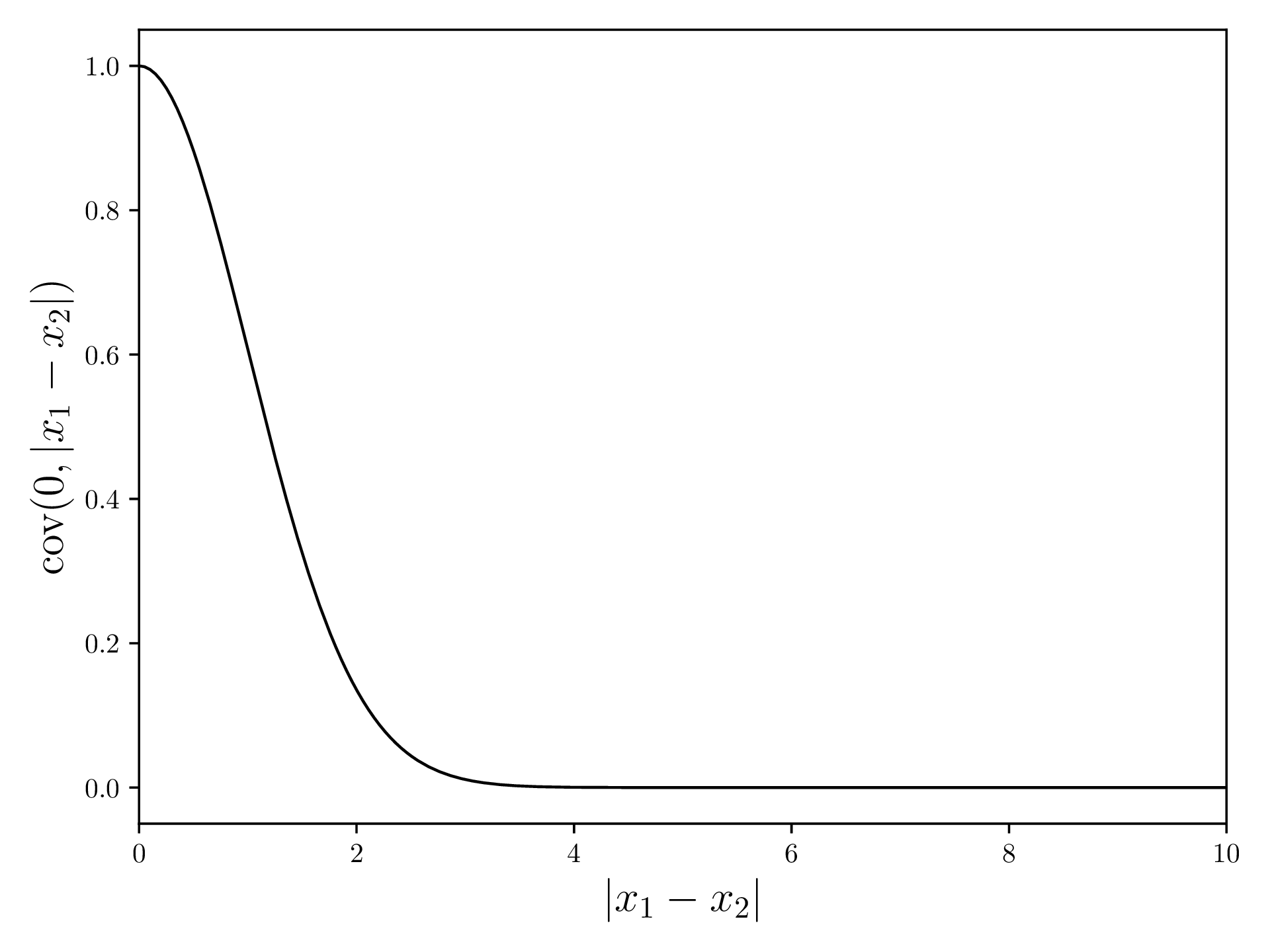
quadratische Exponentialfunktion als Funktion der Distanz zwischen x1 und x2

In Python:

squaredExponentialKernel = lambda x1, x2: np.exp(-np.linalg.norm(x1 - x2)**2 / 2)

Nun schreiben wir eine Funktion, welche eine Kovarianzmatrix aus zwei Inputvektoren x1x_1 und x2x_2 und einer Filterfunktion generiert. Die Kovarianz eines Elements mit sich selbst ist die Varianz.

covariance = lambda x1, x2, kernel: np.array([[kernel(a, b) for b in x2] for a in x1])
In [2]: covariance([1, 2, 3], [1, 2, 3], squaredExponentialKernel)
Out[2]: 
array([[1.        , 0.60653066, 0.13533528],
       [0.60653066, 1.        , 0.60653066],
       [0.13533528, 0.60653066, 1.        ]])

Hier sind 1 und 3 weit auseinander und haben entsprechend eine tiefe Kovarianz.

Gauss-Prozess

Der Gauss-Prozess (als Mittelwert μ\mu und Kovarianz cov\text{cov}) ist definiert als (Quelle )

μ=K(X∗,X)(K(X,X)+I)−1y\mu = K(X_*, X) \left( K(X, X) + I \right)^{-1} \mathbf{y}

und

cov=K(X∗,X∗)−K(X∗,X)(K(X,X)+I)−1K(X,X∗)\text{cov} = K(X_*, X_*) - K(X_*, X) \left( K(X, X) + I \right)^{-1} K(X, X_*)

mit den xx-Werten der Datenpunkte XX, den yy-Werten y\mathbf{y} und den Werten, wo wir den Gauss-Prozess auswerten möchten, X∗X_*.

Nun schreiben wir eine Funktion, welche diese Ausdrücke implementiert. Das machine_epsilon ist der kleinste Wert, welchen ein float32 annehmen kann und verhindert, dass Werte 0 werden, ohne die effektive Berechnung zu stören. Einige Operationen werden fehlerhaft, wenn ein Wert 0 ist.

Nachdem wir μ\mu und cov\text{cov} berechnet haben, berechnen wir die Standardabweichung an jedem Punkt, indem wir die Wurzel der Diagonalelemente (= Varianz) nehmen.

def gaussian_regression(x, y, predict, kernel=squaredExponentialKernel):
    # K(X, X) + I
    K = covariance(x, x, kernel) + machine_epsilon * np.identity(len(x))
    # K(X_*, X)
    Ks = covariance(predict, x, kernel)
    # K(X*, X*)
    Kss = covariance(predict, predict, kernel)
 
    K_inv = np.linalg.inv(K)
 
    mean = np.dot(
        Ks,
        np.dot(
            K_inv,
            y
        )
    )
 
    cov = Kss - np.dot(
        Ks,
        np.dot(
            K_inv,
            Ks.T
        )
    )
 
    cov += machine_epsilon * np.ones(np.shape(cov)[0])
 
    std = np.sqrt(np.diag(cov))
 
    return mean, std

Nun können wir diese Funktion verwenden, um das Surrogatmodell zu berechnen und dieses zu Plotten.

mean, std = gaussian_regression(*samples.T, xvalues, kernel=squaredExponentialKernel)

Ich plotte hier drei Standardabweichungen, um die kleiner werdende Wahrscheinlichkeit einer Messung an einem Punkt zu visualisieren.

fig, ax = plt.subplots(figsize=(12.8, 4.8))
ax.scatter(*np.array(samples).transpose(), s=10, c='black', label=r'samples')
ax.plot(xvalues, objective_function(xvalues), color='black', linewidth=1, label='objective function')
ax.plot(xvalues, mean, linestyle='--', color='black', linewidth=1, label=r'surrogate function')
ax.fill_between(xvalues, mean + std, mean - std, alpha=0.2, color='black', label=r'surrogate function $\sigma$', linewidth=0)
ax.fill_between(xvalues, mean + 2*std, mean - 2*std, alpha=0.15, color='black', label=r'surrogate function $2\sigma$', linewidth=0)
ax.fill_between(xvalues, mean + 3*std, mean - 3*std, alpha=0.1, color='black', label=r'surrogate function $3\sigma$', linewidth=0)
 
ax.set_xlim(*DOMAIN)
ax.set_xlabel(r'$x$', fontsize=16)
ax.set_ylabel(r'$f(x)$', fontsize=16)
 
ax.legend()
plt.tight_layout()
plt.savefig(os.path.join('output', f'gaussian_regression.pdf'))
plt.close('all')
Surrogate model with mean and standard deviation for three points

Akquisitionsfunktion

Um Erwartete Verbesserung zu verstehen, macht es Sinn, sich zuerst “Wahrscheinlichkeit der Verbesserung” (PI, engl. “Probability of Improvement”) anzuschauen.

Für einen aktuell besten Messwert (x∗x^* und f(x∗)f(x^*)) definiert PI eine Funktion I(x)I(x), die die Wahrscheinlichkeit beschreibt, dass ein neuer gemessener Punkt an xx besser wird als der aktuell beste Punkt. Dafür definiert das Surrogatmodell vom ersten Schritt eine Normalverteilung in Richtung yy für jedes xx, welches durch die grauen Flächen dargestellt wird.

Visualisierung von PI, neu gezeichnet von hier :

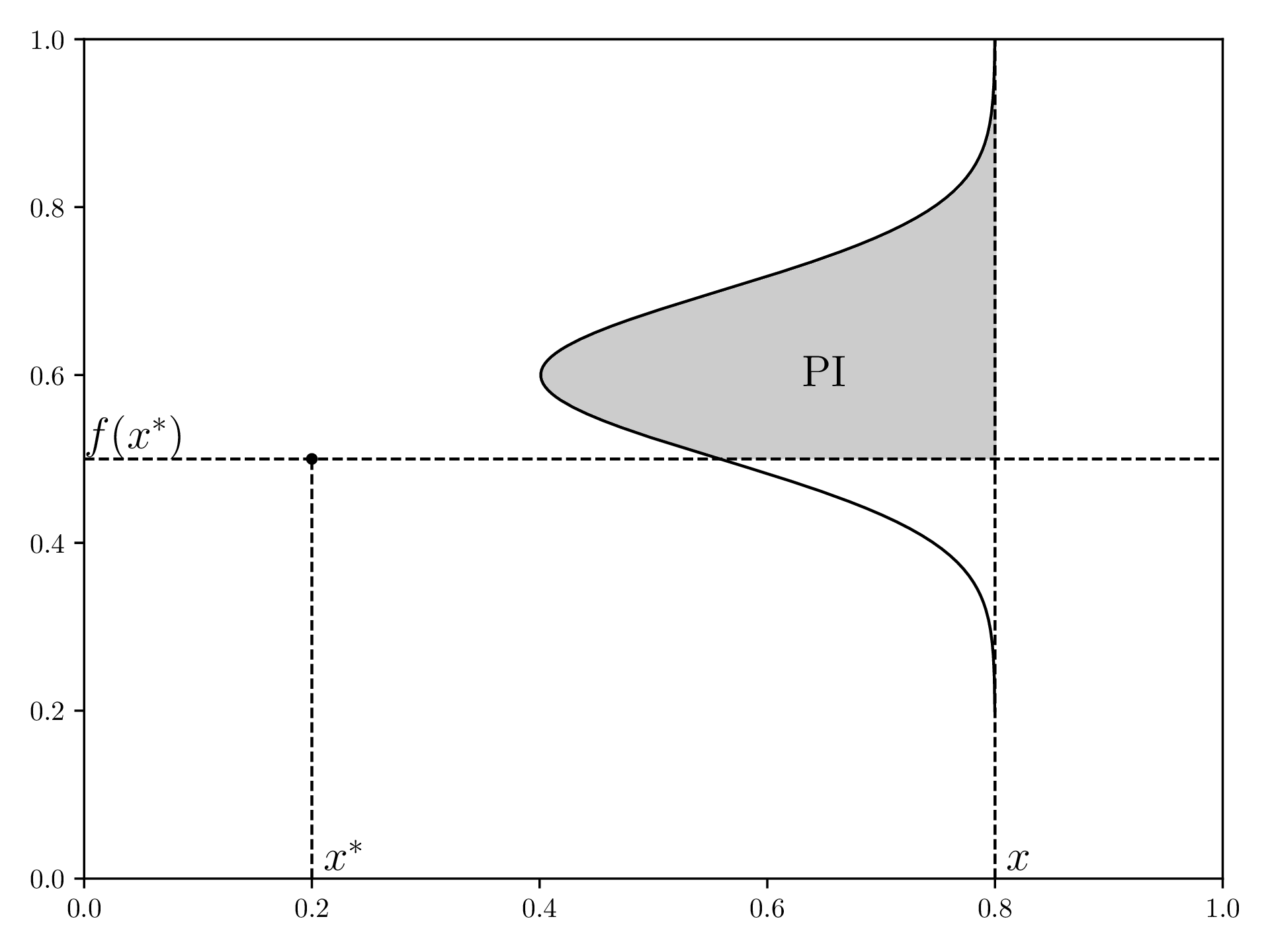
Visualisierung von PI

EI schaut sich jetzt nicht nur an, ob eine Messung die beste Messung verbessern wird, sondern auch um wie viel.

Um EI zu implementieren, müssen wir zunächst wissen, welcher Punkt der aktuell Beste ist. Dafür können wir die reduce Funktion verwenden:

best_point = reduce(lambda point, m: point if point[1] > m[1] else m, samples)

reduce ist eine Funktion, welche man in der funktionellen Programmierung of verwendet und reduziert eine Liste auf einen Wert. Dafür nimmt reduce einen Funktion, welche wiederum einen Wert und einen Akkumulator nimmt und einen neuen Akkumulator zurückgibt.

EI ist definiert durch (Quelle )

EI(x;ξ)=δΦ(δσ)+σφ(δσ)\text{EI}(x; \xi) = \delta \Phi\left(\frac{\delta}{\sigma}\right) + \sigma\varphi\left(\frac{\delta}{\sigma}\right)

mit δ=μ−f(x∗)−ξ\delta = \mu - f(x^*) - \xi, der Wahrscheinlichkeitsdichte der Normalverteilung φ\varphi (scipy.stats.norm.pdf) und der Kumulativen Wahrscheinlichkeitsdichte der Normalverteilung Φ\Phi (scipy.stats.norm.cdf).

Der Parameter ξ\xi konrolliert “Erkundung und Ausnutzung”: Wenn ξ\xi nah bei 0 ist, wird BO oftmals versuchen, ein lokales Optimum zu finden und konvergiert entsprechend schneller, mit dem Risiko, dass das lokale Optimum nicht das Globale ist. Grosse ξ\xi führen dazu, dass BO mehr “herumspringt” und entsprechend Punkte evaluiert, die weiter weg vom vorherigen Punkt sind.

Um das zu schreiben, definieren wir zuerst eine leere Liste EI und loopen dann über alle Punkte, um EI(x)\text{EI}(x) zu berechnen. Beachte dass scipy.stats.norm eine Klasse ist und wir zuerst ein Objekt mit der Standardabweichung instanzieren müssen.

xi = 0.1
 
EI = []
for i in range(len(xvalues)):
    delta = mean[i] - best_point[1] - xi
    std[std == 0] = np.inf
    z = delta / std[i]
    unit_norm = norm(scale=std[i])
    EI.append(delta * unit_norm.cdf(z) + std[i] * unit_norm.pdf(z))

Nun können wir EI plotten:

fig, ax = plt.subplots(figsize=(12.8, 4.8))
ax.plot(xvalues, EI, linewidth=1, color='black')
 
ax.set_xlim(*DOMAIN)
ax.set_xlabel(r'$x$', fontsize=16)
ax.set_ylabel(r'$\text{EI}$', fontsize=16)
 
plt.tight_layout()
plt.savefig(os.path.join('output', f'expected_improvement.pdf'))
plt.close('all')
Erwartete Verbesserung der Surrogatfunktion oben

Neue Messung

Zuletzt finden wir das Maximum von EI und benutzen dessen xx-Wert, um einen neuen Datenpunkt zu messen. Wir fügen dann diesen [x, y] Datenkpunkt zum samples-Array hinzu.

max_EI_index = np.argmax(EI)
max_EI = EI[max_EI_index]
 
samples = np.array([*samples, [xvalues[max_EI_index], objective_function(xvalues[max_EI_index])]])

Maximum Zurückgeben

Die Schritte Surrogatmodell, Akquisitionsfunktion und Neue Messung werden nun BUDGET Mal wiederholt.

Danach können wir das Surrogatmodell nochmal generieren und dessen Maximum finden.

mean, std = gaussian_regression(*samples.T, xvalues, kernel=squaredExponentialKernel)
max_index = np.argmax(mean)
 
print(f"Maximum found at {[xvalues[max_index], mean[max_index]]}")
Surrogatmodell nach 10 Iterationen

Kompletter Code

Die Schritte im Loop sind hier Teil des Hauptloops und generieren für jede Iteration einen Plot mit dem Iterator im Dateinamen. Die zero_pad Funktion stellt einfach sicher, dass jeder Iterator dieselbe Anzahl an Ziffern hat (z.B. 0024), was korrekte Sortierung von deinem OS erlaubt.

import os
import numpy as np
import matplotlib.pyplot as plt
 
from functools import reduce
from scipy.stats import norm
 
DOMAIN=[0,10]
INITIAL_SAMPLES=3
BUDGET=10
 
machine_epsilon = np.finfo(np.float32).eps
 
objective_function = lambda x: np.sin(1.7 * x) + np.cos(x)
samples = np.array([[x, objective_function(x)] for x in np.linspace(*DOMAIN, INITIAL_SAMPLES+2)[1:-1]])
 
 
# --- Objective Function ---
fig, ax = plt.subplots(figsize=(12.8, 4.8))
 
xvalues = np.linspace(*DOMAIN, 200)
yvalues = objective_function(xvalues)
 
ax.plot(xvalues, yvalues, linewidth=1, color='black')
ax.scatter(*samples.T, s=10, c='black')
ax.set_xlabel(r'$x$', fontsize=16)
ax.set_ylabel(r'$f(x)$', fontsize=16)
ax.set_xlim(*DOMAIN)
 
plt.tight_layout()
os.makedirs('output', exist_ok=True)
plt.savefig(os.path.join('output', 'objective_function.pdf'))
plt.close('all')
 
 
# --- Covariance ---
squaredExponentialKernel = lambda x1, x2: np.exp(-np.linalg.norm(x1 - x2)**2 / 2)
covariance = lambda x1, x2, kernel: np.array([[kernel(a, b) for b in x2] for a in x1])
 
yvalues = [squaredExponentialKernel(0, x) for x in xvalues]
 
plt.plot(xvalues, yvalues, color='black', linewidth=1)
 
plt.xlim(*DOMAIN)
plt.xlabel(r'$|x_1 - x_2|$', fontsize=16)
plt.ylabel(r'$\text{cov}(0, |x_1 - x_2|)$', fontsize=16)
 
plt.tight_layout()
plt.savefig(os.path.join('output', 'squaredExponentialKernel.pdf'))
plt.close('all')
 
 
# --- Gaussian Regression ---
def gaussian_regression(x, y, predict, kernel=squaredExponentialKernel):
    K = covariance(x, x, kernel) + machine_epsilon * np.identity(len(x))
    Ks = covariance(predict, x, kernel)
    Kss = covariance(predict, predict, kernel)
 
    K_inv = np.linalg.inv(K)
 
    mean = np.dot(
        Ks,
        np.dot(
            K_inv,
            y
        )
    )
 
    cov = Kss - np.dot(
        Ks,
        np.dot(
            K_inv,
            Ks.T
        )
    )
 
    cov += machine_epsilon * np.ones(np.shape(cov)[0])
 
    std = np.sqrt(np.diag(cov))
 
    return mean, std
 
def zero_pad(value, max_number):
    num_digits = int(np.log10(max_number-1)) + 1
    return str(value).zfill(num_digits)
 
for i in range(BUDGET):
    print(f"==> Iteration {i+1}/{BUDGET}")
    filename_suffix = zero_pad(i, BUDGET)
 
 
    # --- Surrogate Model ---
    mean, std = gaussian_regression(*samples.T, xvalues, kernel=squaredExponentialKernel)
 
    fig, ax = plt.subplots(figsize=(12.8, 4.8))
    ax.scatter(*np.array(samples).transpose(), s=10, c='black', label=r'samples')
    ax.plot(xvalues, objective_function(xvalues), color='black', linewidth=1, label='objective function')
    ax.plot(xvalues, mean, linestyle='--', color='black', linewidth=1, label=r'surrogate function')
    ax.fill_between(xvalues, mean + std, mean - std, alpha=0.2, color='black', label=r'surrogate function $\sigma$', linewidth=0)
    ax.fill_between(xvalues, mean + 2*std, mean - 2*std, alpha=0.15, color='black', label=r'surrogate function $2\sigma$', linewidth=0)
    ax.fill_between(xvalues, mean + 3*std, mean - 3*std, alpha=0.1, color='black', label=r'surrogate function $3\sigma$', linewidth=0)
 
    ax.set_xlim(*DOMAIN)
    ax.set_xlabel(r'$x$', fontsize=16)
    ax.set_ylabel(r'$f(x)$', fontsize=16)
 
    ax.legend()
    plt.tight_layout()
    plt.savefig(os.path.join('output', f'gaussian_regression_{filename_suffix}.pdf'))
    plt.close('all')
 
 
    # --- Acquisition Function ---
    best_point = reduce(lambda point, m: point if point[1] > m[1] else m, samples)
    xi = 0.1
 
    EI = []
    for i in range(len(xvalues)):
        delta = mean[i] - best_point[1] - xi
        std[std == 0] = np.inf
        z = delta / std[i]
        unit_norm = norm(scale=std[i])
        EI.append(delta * unit_norm.cdf(z) + std[i] * unit_norm.pdf(z))
 
    fig, ax = plt.subplots(figsize=(12.8, 4.8))
    ax.plot(xvalues, EI, linewidth=1, color='black')
 
    ax.set_xlim(*DOMAIN)
    ax.set_xlabel(r'$x$', fontsize=16)
    ax.set_ylabel(r'$\text{EI}$', fontsize=16)
 
    plt.tight_layout()
    plt.savefig(os.path.join('output', f'expected_improvement_{filename_suffix}.pdf'))
    plt.close('all')
 
    # --- measure another sample ---
    max_EI_index = np.argmax(EI)
    max_EI = EI[max_EI_index]
 
    samples = np.array([*samples, [xvalues[max_EI_index], objective_function(xvalues[max_EI_index])]])
 
 
# --- get maximum of surrogate model ---
mean, std = gaussian_regression(*samples.T, xvalues, kernel=squaredExponentialKernel)
max_index = np.argmax(mean)
 
print(f"Maximum found at {[xvalues[max_index], mean[max_index]]}")

Comments

Source Code

Subscribe via RSS.

MIT 2025 © Alexander Schoch.